Prof. dr hab. inż Tadeusz Orzechowski, Politechnika Świętokrzyska w Kielcach
Rzeczywiste procesy w układach zmiennofazowych są bardzo skomplikowane. Z tego względu modelowanie zachowania się takich układów wymaga indywidualnego opisu uwzględniającego właściwości PCM, geometrię układu oraz usytuowanie zasobnika w instalacji.
Celem niniejszej pracy jest propozycja prostego modelu obliczeniowego, który przy pewnych założeniach ma rozwiązanie analityczne, co ma szczególnie znaczenie w praktyce inżynierskiej. Przedmiotem rozważań jest modelowanie pracy zasobnika zmiennofazowego do współpracy ze źródłem lub odbiornikiem energii cieplnej. Geometrię zasobnika przedstawiono na rysunku 1. Zakłada się, że jest on dobrze izolowany od otoczenia tak, że straty ciepła do otoczenia są pomijalnie małe. Ze względu na niską przewodność PCM oraz odpowiednio gęsty rozstaw kanałów, którymi płynie nośnik ciepła, pomija się strumień ciepła wzdłuż długości, którą dla wygody zastąpiono powierzchnią bieżącą wymiennika F. Wymiana ciepła pomiędzy nośnikiem, a materiałem akumulującym zachodzi jedynie na powierzchni ich rozdziału, gdzie znany jest współczynnik przenikania ciepła U.
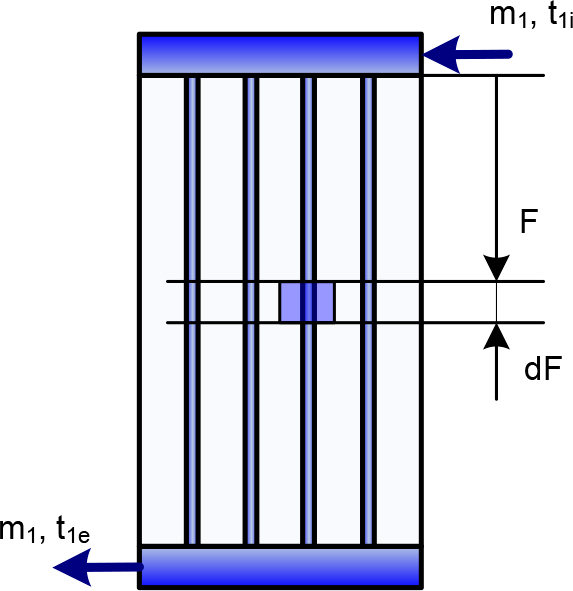
Z bilansu ciepła dla elementarnej objętości układu przedstawionego na rysunku 1 wynikają następujące równania opisujące rozkład temperatury nośnika ciepła T1 oraz PCM T2. Obydwie wielkości są funkcją czasu t i powierzchni F.
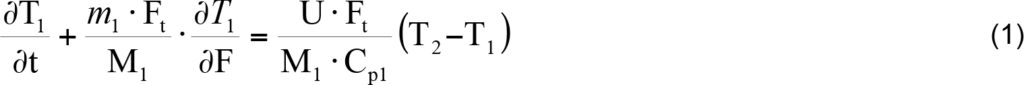

gdzie wskaźniki 1, 2 odnoszą się odpowiednio do nośnika ciepła i zmiennofazowego materiału akumulującego, Ft – jest całkowitą powierzchnią wymiany ciepła, M1 – masa PCM w zasobniku, m1 – strumień masy nośnika ciepła, Cp – ciepło właściwe.
Dodatkowo założono, że wymiana ciepła towarzysząca procesom konwekcji swobodnej występująca przy niejednorodnym rozkładzie temperatury wzdłuż wysokości zasobnika jest pomijalnie mała w porównaniu z ciepłem wymienianym pomiędzy obydwiema substancjami, tj. materiałem akumulacyjnym i przepływającym nośnikiem ciepła.
W ogólnym przypadku powyższy układ równań jest nieliniowy, który – po zadaniu warunków początkowych i brzegowego – może być efektywnie rozwiązany numerycznie. Warto zaważyć, że ich prawe strony mają taką samą postać liniowej zależności od różnicy temperatury pomiędzy przepływającym nośnikiem ciepła i materiałem akumulacyjnym. Po sprowadzeniu tego układu do postaci bezwymiarowej można wykazać następującą relację:

W takim przypadku pochodna temperatury nośnika ciepła po czasie w pierwszym równaniu może być pominięta, a równanie (1) przyjmie poniższą postać:

Zależności (2) i (4) stanowią układ równań opisujących niestacjonarny rozkład temperatury w zasobniku. Ilustrację przykładowego procesu ładowania zasobnika z parafiną ze źródła o stałej w czasie temperaturze T1=T10=90oC pokazano na rysunku 2.

Dla zasobnika o masie PCM (parafina) M2=50 kg i początkowej temperaturze T20=20o C, przy pojemności wewnętrznej nośnika ciepła (woda) w ilości M1=1 kg i strumieniu masowym m1=0.02 kg/s stwierdzono, że błąd względny wynikający z poczynionych uproszczeń wynosi około 1,65 proc. dla bezwymiarowej temperatury T1/T20 i odpowiednio 2,6 proc. dla T2/T20. Obliczenia te pokazują, że już przy stosunku mas M2/M1=50 można pominąć pochodną lokalną w równaniu opisującym rozkład temperatury nośnika ciepła, a poczyniony błąd w obliczeniach w takim przypadku jest stosunkowo niewielki.
Ładowanie zasobnika z wkładem PCM o dużej masie
Zastosowanie zbiornika akumulującego ciepło pracującego przy zmianie fazy czynnika wymaga ograniczenia negatywnego wpływu niskiej przewodności substancji zmiennofazowej. Można to osiągnąć poprzez dobre rozwiniecie powierzchni biorących udział w wymianie ciepła, co – przy odpowiedniej konstrukcji zasobnika – skutkuje jednakową temperaturą w całej objętości zasobnika. Przyjęcie jednakowej temperatury w całej objętości zbiornika nie wprowadza znaczących błędów w obliczeniach wtedy, kiedy liczba Biota jest mała. Dla obliczeń inżynierskich wystarczy Bi<0,1 [1].
Przy przyjętych założeniach lokalny bilans ciepła prowadzi do następującej zależności:

które opisuje zmianę temperatury wewnątrz zasobnika w funkcji czasu T2=T2(t). Prawa strona tego równania jest ciepłem wymienianym pomiędzy nośnikiem, a PCM w zasobniku i jest proporcjonalna do różnicy temperatury nośnika ciepła na wejściu do T1(t,0)=T10 i wyjściu z zasobnika T1(t,Ft).
W przypadku odpowiednio dużego stosunku M2/M1 równanie na rozkład temperatury wzdłuż długości zasobnika można – jak pokazano wyżej – w postaci (4), tj.:
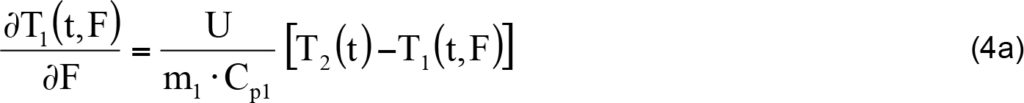
Przy przyjętych założeniach, w powyższym równaniu czas t jest parametrem, a temperatura zbiornika T2= T2(t) i nie zależy od powierzchni F, zależność (4) można łatwo scałkować. Przyjmując, że na wlocie do zbiornika jest dana temperatura czynnika zasilającego T10 otrzymujemy:

Warto zwrócić uwagę, że zależność temperatury nośnika T1 od czasu jest zależnością pośrednią poprzez T2(t). Wykorzystując powyższe w równaniu (3) otrzymujemy następujące jego rozwiązanie:

gdzie E jest stałą określaną wzorem:
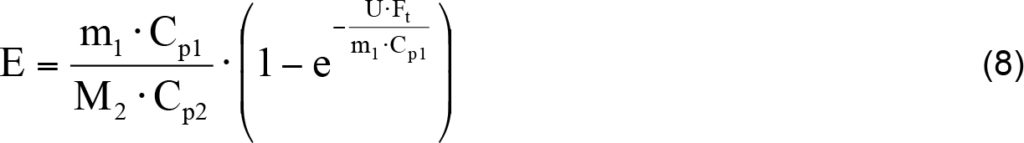
Przy całkowaniu wykorzystano warunek początkowy, przyjmując, że znana jest temperatura zbiornika na starcie procesu ładowania T2(t=0)=T20.
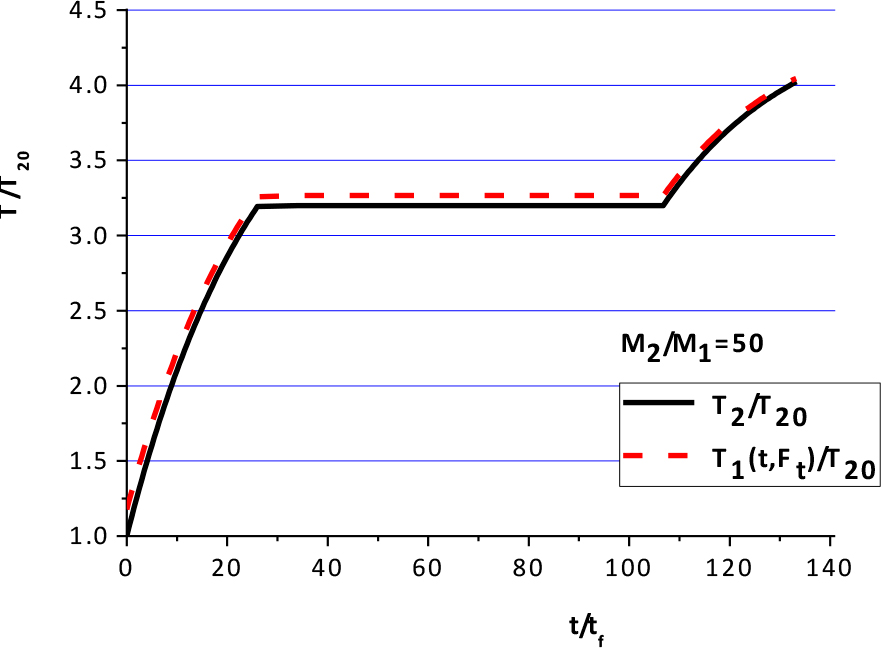
Rys. 3. Zmiana temperatury zbiornika z PCM
oraz nośnika ciepła na wypływie w funkcji czasu
Widoczna na rysunku 3 niewielka różnica pomiędzy temperaturą T2 w zbiorniku z PCM a temperaturą T1(t,Ft) na wylocie ze zbiornika świadczy o poprawnym doborze strumienia cieczy zasilającej (tutaj m1=0,02 kg/s). Jego zwiększenie skutkuje zwiększeniem różnicy tych temperatur, a więc i dłuższym czasem nagrzewania przy zwiększonych oporach przepływu, co jest zjawiskiem niekorzystnym.

Rys. 4. Rozkład temperatury cieczy grzewczej w zasobniku dla różnych czasów
w początkowym okresie akumulacji
Podsumowanie i wnioski
Zapoczątkowane działania ograniczenia zużycia nieodnawialnych nośników energii o przynajmniej 20% w najbliższych latach wymagają wielu technologicznie nowatorskich rozwiązań. Jednym z możliwych jest szersze zastosowanie akumulacji energii, w tym cieplnej niskotemperaturowej. Jej zasób jest ogromny, lecz jej efektywne wykorzystanie jest ograniczone okresową dostępnością: krótkoterminową i długoterminową. W pracy wprowadzono prosty układ równań, który opisuje proces ładowania lub rozładowania zasobnika z wypełnieniem PCM w przypadku niestacjonarnym i jednowymiarowym. Omówiono możliwe uproszczenia tak, aby otrzymać zależności do wykorzystania w praktyce inżynierskiej. Wskazano również na błędy czynionych założeń upraszczających, które zależne są od stosunku masy substancji akumulującej do masy czynnika grzewczego pozostającego w zasobniku.
Modelowanie procesów ładowania i rozładowania zasobnika akumulującego z materiałem zmiennofazowym w instalacjach ze źródłem o okresowej dostępności zezwala na poszukiwanie optymalnych parametrów pracy i dobór charakterystyk sterowania [2].
Fot. Pixabay
Literatura:
[1] Incropera F.P. at al. Fundamentals of Heat and Mass Transfer. John Wiley & Sons. 2007
[2] Orzechowski T., Stokowiec K.: Heat storage tank operation with a phase change bed –numerical calculations. The 15th Conference for Junior Researches Science for Future. Engineering Systems for Building. 12-13 April 2012. Vilniaus Gedimino technikos universitetas. 93-97.